Question:
A particle of mass m is attached between two horizontal springs of stiffness 2k and 5k, each of un-stretched length a (see figure below). The mass is held stationary at a displacement from its resting position of x = 1.03m.
Show that the system satisfies the differential equation given by:
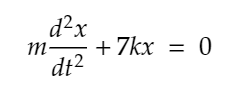
and use Laplace transforms of derivatives to find L{x}.
Answer:
Resolving horizontally (+ve direction from left to right):
Take Laplace transforms of both sides:
Sub in Laplace transform of derivatives:
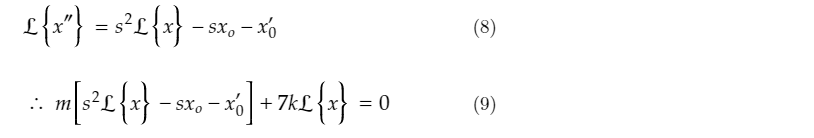
Sub in initial conditions x0 and x'0:
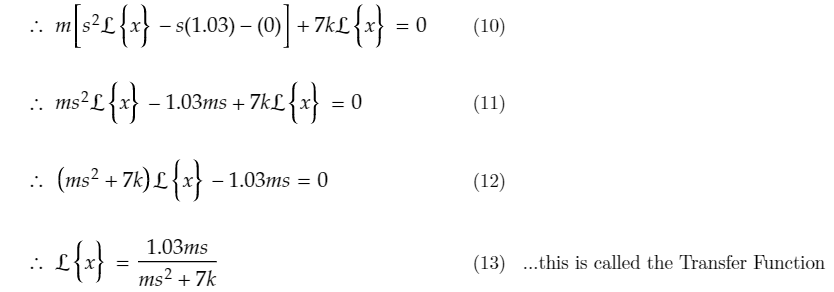
Question:
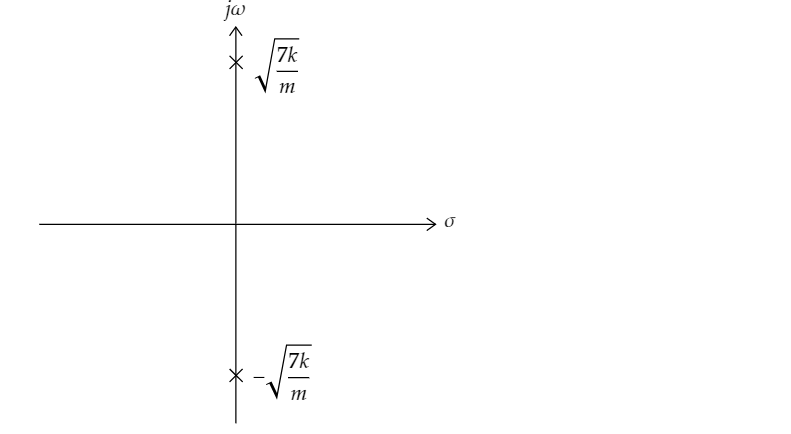
Determine the poles and zeros of the system and plot them on a pole-zero diagram. Use the initial value theorem to check your Laplace Transform.
Answer:
Find the Poles:
Find the Zeros:
Draw the Pole-Zero diagram:
Determine initial values:
We know this is correct as the displacement at time = 0 was known.
Question:
By using tables to find the Inverse Laplace Transform, determine the equation for the displacement x(t)
Inverse Laplace:
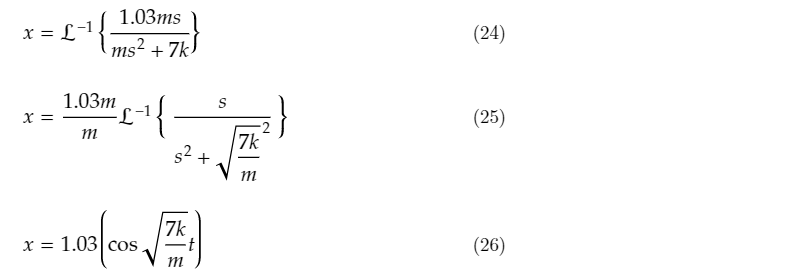
Comments